机械臂运动学求解概述
应用场景即其目的
在机器人设计及其控制中,往往认为机器人主要由三种组件构成,即感知器件、执行器件和智能器件。而机械臂作为执行器件中非常重要的一种给机器人提供了更具灵活性的改造世界的能力。
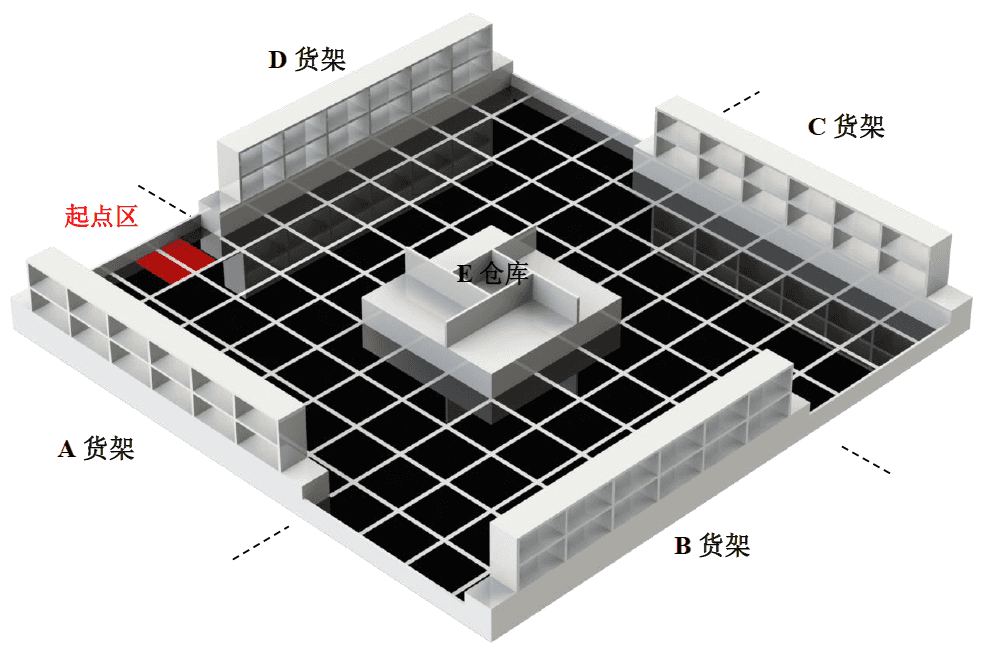
例如在以下场景中,我们需要将位于D货架某一点的“商品”移动至机器人背后的购物车上或者从某一个货架移动至另一个货架。
图1. 机械臂应用场景图
在这种场景中,机械臂无疑是一种非常适合且方便通用的执行部件。除此之外还有其他的装配、焊接、服务等等各类不同的场景可以使用。需要注意的是,不同应用场景对机械臂运动的精度、移动范围、机械手操作能力都有不同的需求,不可一概而论。
例如,在上述这个简单的比赛场景中,物品都放在货架每一格的固定位置,因为条件固定,对象单一,最高效也最简单的机械臂控制方法就是if-else控制。即:假设机器人位于货架某一格的正前方,对于可能存在的若干个位置设定不同的机械臂驱动量,使得机械手刚好位于目标位置,一过程只需要进行适当的人工调试即可找到适合的驱动量。同理,放到对应的位置也可按照上述方法。
但是,如果物品的位置不固定呢?显然,这一方法将彻底失效,因为你很难为机械臂运动范围内的每一点进行调试,同时这些一一对应的数据的保存也需要不少的存储空间,因此,再用人工调试的方法无疑是费力不讨好且不现实的。
这时,机械臂的运动学计算 就显得格外重要了。
什么是运动学计算?
假设给定一机械臂如下:
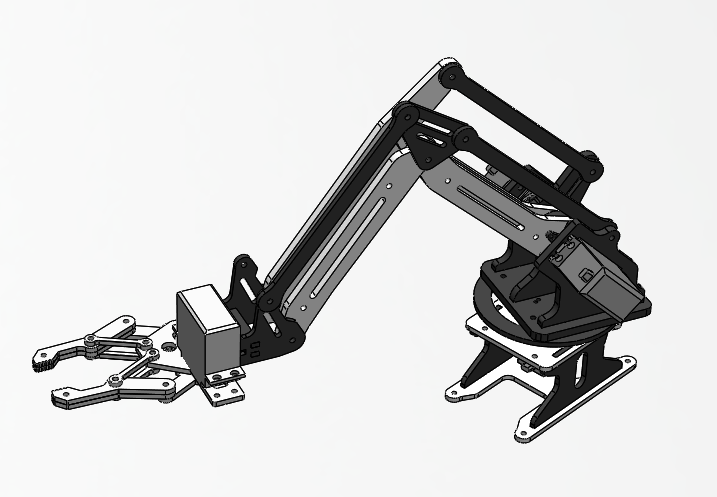
图2. 机械臂模型图
根据上图可以很容易可以看出机械臂是一种仿生手臂的执行部件,具备关节、臂、手等结构。臂为固定长度的连杆,不发生形变;关节可以绕一定的轴进行有限制或无限制的旋转;手可以提供抓持能力。
那么假如我设计一套算法,它提供了给定各个关节的角度即可计算得到机械手位置的能力,那么一定能给机械臂控制带来一定的便捷,而这就是正向运动学计算。通过一定的空间几何数学知识可以得到,这显然是可行的。
假设机械臂一共有四个关节,四个关节的角度分别为$ \theta_1 $、$ \theta_2 $、$ \theta_3 $和$ \theta_4 $,机械手末端的空间坐标为$ \boldsymbol P = \left( x,y,z \right) $。那么这一算法可以用数学表述为
$$ \label{一般正向运动学公式} \tag{1} \boldsymbol P = f \left( \theta_1 , \theta_2 , \theta_3 , \theta_4 \right) $$
显然,正向运动学在实际应用中还不够实用,但假如我对上式进行一定的数学变换,即可得到如下方程组:
$$ \begin{cases} \label{一般逆向运动学公式} \tag{2} \theta_1 = g_1 \left( x , y, z \right) \\ \theta_2 = g_2 \left( x , y, z \right) \\ \theta_3 = g_3 \left( x , y, z \right) \\ \theta_4= g_4 \left( x , y, z \right) \end{cases} $$
这就是机械臂的逆向运动学计算,即给定机械手的空间坐标,计算得到各个关节应当转动到的角度。显然,比起正向运动学计算,逆向运动学的应用更广泛。因为我们往往是获知目标点后操作机械臂去抓取。
但是,对式$\eqref{一般正向运动学公式}$式$\eqref{一般逆向运动学公式}$进行分析,因为坐标$P$有三个变量,这意味着式$\eqref{一般正向运动学公式}$是一个有三个方程的方程组,假设我们把该式中的$ x $、$ y $、$ z $看作已知量,那么式$\eqref{一般逆向运动学公式}$的求解就成为了根据三个方程求解四个变量$ \theta_1 $、$ \theta_2 $、$\theta_3 $、$\theta_4 $,我们会发现这一数学变换是非常困难的。
该机械臂有四个关节,即具有四个自由度。我们把自由度定义为独立对物理状态结果产生影响的变量的数量,通俗的来讲就是能提供几个维度的变化,或者说系统的输出受到几个变量的影响,如果机械臂每个关节只能绕一个轴旋转,因此只有一个变量,那么四个关节一共就是四个变量,也就是四自由度。假设某机械臂只有一个关节,那么他的运动范围可能只有一个圆弧,显而易见,它的自由度非常的有限,此时它的输出方程为:
$$ y = f \left( x \right) $$
实际上,对于四自由度机械臂的逆向运动学求解也并非是无解的,使用三个方程并非不能求解出四个未知数。更准确的说是解的数量是无穷的。虽然该方程组不一定是线性的,但解的情况和线性方程组的解的种类有相同之处。
一般应用场景中,无穷解并不是什么问题,因为在计算机求解中往往并不关心解析解,只要我们能够找到符合方程条件并达到足够精度的数值解即可满足我们的使用要求。除了某些极端的极限精度领域,谁会在乎我保留了小数点后面的七八位还是给出了精准的无理数结果呢?更别说常规编程中如果不融入符号运算或者其他自定数据类型,double变量也不过15位有效数字。
除了利用搜索算法寻找满足条件的解析解,还有一种就是对自由度加以约束即可得到唯一解,例如我们人为的加入一个方程:
$$ \theta_4 = f \left( \theta_1 , \theta_2 , \theta_3 \right) $$
这样,我们就得到了四个方程,也就确保了四个自由度机械臂在给定末端空间三维坐标的时候具有唯一解。这将给后续的应用和可行性分析提供很大的方便。
这种情况我们称为带约束的四自由度机械臂运动学求解 。其本质上是通过一个约束使得四自由度机械臂变成了三个自由度。(如果你不在乎丢失一个自由度或者机械臂本来就只有三个自由度的话)
实际上,机械臂的运动学计算已经有了非常一般性的计算方法,适合于各类连杆结构甚至变连杆结构的机械臂,其主要将机械臂的每一端手臂视为一个连杆,并给定连杆长、连杆扭角、两连杆距离、两连杆夹角等参数,并利用齐次坐标变换的知识,将机械臂各个关节的坐标从关节空间逐级变换至原点笛卡尔空间。这是一般性的计算方法,具有广泛的普适性,但不是本文的讨论内容。
本文将以简单结构的四自由度机械臂为例,利用最简单的数学几何知识进行求解,过程并不复杂,也没有包含什么知识,只是希望能够给读者提供一点微薄的帮助 。
机械臂结构分析
对机械臂进行运动学计算的基础是对其结构进行分析。
本文分析的机械臂如图1所示,我们对其进行适当的抽象后得到下图:
图3. 机械臂结构抽象图(左:整体示意图,中:正视图,右:俯视图)
上图左图中的矩形为云台(也是一种关节),大圆形为普通关节,菱形为机械手,粗直线为臂,细直线及小圆形为约束机构,虚线框起来的部件为一个整体。上图的中图和右图是对机械臂进行进一步抽象后的正视图和俯视图,并对各个角度和长度进行了严格定义,其中角度均以极坐标为标准,即逆时针方向为正,且夹角均为当前臂按逆时针方向为正的原则从上一臂延长线转向当前位置的关节角。
需要说明的是,对角度定义的统一有利于后续分析的一般化,特别是正负方向的定义,这一点在下文的具体分析中会再次强调。因为如果夹角及其方向的选取过于任意且不统一,可能导致分析的公式较为特殊,不具有一般性,当角度小于零度或者大于一百八十度是可能需要应用不同的公式等等。
约束机构分析
图4. 约束机构分析
这是一个自带约束机构的机械臂,其中存在的两个平行四边形机构保证了对边平行。即$l_1 // l_2$、$l_4 // l_6$,又由于 $l_1$ 固定在机械臂上,且与云台平面夹角不变,因此$l_2$ 与云台平面夹角同样为一定值,同时, $l_2$、$l_3$和$l_4$组成的三角形是稳定结构,其三个内角均不变,只要三角形形状合适,可以使得 $l_3$始终与云台平面平行。
类似的分析,$l_4 // l_6$ ,$l_6 $和$l_7 $夹角固定,若三角形形状合适,可以使得$l_7 // l_3 // 云台平面$。
总的来说,这个约束机构保证了$l_7 $与水平面平行(除非机械臂不是水平安装),那么这必然导致关节角$\gamma$受到约束,我们对其进行几何分析可得:
图5. 约束角度分析图
上图中有$\gamma = \angle 1 = \beta – \angle 2 $ ,$ \angle 2 + \angle 3 = \frac{\pi}{2} $ ,$ \angle 3 = \alpha $,对上述三式联立可得:
$$ \gamma = \frac{\pi}{2} – \alpha – \beta $$
至此,我们得到了关节角$\gamma$的约束式。
显然,这是一个具有四个关节和一个机械手,但自由度为3+1的一个四自由度机械臂,如果我们假定机械手的张合不改变机械臂末端的空间坐标的话(因为抓持往往使用机械手的中点),这就是一个“三自由度”的机械臂。
其实,后文的运动学计算会发现这一约束式的得出是无必要的,因为这一角度约束式和平行约束关系$l_7 // 云台平面$完全等价,后面的计算将直接使用这一平行关系。
正向运动学计算
对机械臂(图1和图3)进行分析并作辅助线如下:
图6. 正向运动学分析几何图(侧面)
上图中所有的辅助线均为水平线、竖直线或臂的延长线,不再作详细说明。$P_0$至$P_4$分别为机械臂的各个抽象关节的端点,坐标分析将基于端点进行。
需要说明的是,根据对机械臂(图1)舵机安装位置的分析,我们可以判断舵机安装在上图$\angle b$和$\angle s$的位置,即机械臂的直接驱动杆为与这两个角相邻的杆。因此这两个角是最基本的变量,其他的角度都受这两个角控制,是关于这两个角的函数,也就是说这两个角可以视为基。我们后续分析的最终目的是把一切变量都化为关于这两个角的函数式,这有利于单片机的直接驱动。
现在对图6进行继续分析,由前述平行关系易得$\angle 1 = \angle s $,利用三角函数知识易得
$$ \begin{cases} d_1 = a_1 \cos b \\ d_2 = a_2 \cos s \\ d_4 = a_1 \sin b \\ d_3 = a_2 \sin s \end{cases} $$
若记$P_0$为原点,竖直向上为$z’$轴正方向,水平向前为$x’$轴正方形,则可得$P_4$坐标为
$$ \begin{equation} \begin{cases} \begin{aligned} x’ & = d_1 + d_2 + a_3 + a_4 \\ & = a_1 \cos b + a_2 \cos s + a_3 + a_4 \\ z’ & = d_4 – d_3 \\ & = a_1 \sin b – a_2 \sin s \end{aligned} \end{cases} \end{equation} \label{正向运动学方程二维} \tag{3} $$
图7. 正向运动学分析几何图(3维正交直角坐标系)
除了前述两个角外,还有一个角度为云台的旋转角,给机械臂提供了第三个自由度。上图中$P_4$为机械臂末端端点,易得$P_4$的坐标满足:
$$ \begin{equation} \begin{cases} \begin{aligned} x & = D \cos \lambda \\ y & = D \sin \lambda \\ z & = a_1 \sin b – a_2 \sin s \\ D & = a_1 \cos b + a_2 \cos s + a_3 + a_4 \end{aligned} \end{cases} \end{equation} \label{正向运动学方程} \tag{4} $$
最后的第四个自由度为机械手的加持角,本例假定被抓持物位于机械手中点位置,暂时不考虑加持时手末端增长的3-6cm(因为不打算使用手尖拿东西,而是手心)。
实际上,关于最后从二维平面旋转到三维空间的转换,更一般的做法是使用旋转矩阵,但考虑到为了这一小步计算给C语言加入矩阵库有点多余,暂且不用,以简单为要。
我们可以看到式$\eqref{正向运动学方程}$与式$\eqref{一般正向运动学公式}$的形式是类似的,即得到了$x$、$y$、$z$关于角度基向量的方程。因此,我们可以认为式$\eqref{正向运动学方程}$就是该机械臂的正向运动学方程,可以利用该方程直接通过当前关节角计算出现在机械臂所处的空间位置。
逆向运动学计算
逆向运动学的求解一般有四种典型方法:解析法,欧拉法,搜索法和几何法。
对于前述结果,其实这四种方法都可以使用,解析法就是根据显示表达式$\eqref{正向运动学方程}$直接求解出需要的方程,如果显式表达式的得出是根据前文所述的齐次坐标变换得到的,那么可以直接利用线性代数的知识对各个齐次变换矩阵求逆后左乘即可。而欧拉法则基于欧拉角(俯仰角、航向角、横滚角)展开,搜索法为计算机求解方法,适合于多自由度多解的求解。
本例的机械臂结构较为简单,且存在唯一定解,可以使用几何法直接逆向分析。(实际上我尝试了使用MATLAB工具直接进行求解,但是由于方程过于冗长,且尝试了几组数据结果均不成立,遂采用几何法进行分析,MATLAB求解的公式贴于文末附录A)
几何法的逆向运动学分析如下:
首先,$P_4$坐标为已知量,记为$ P_4 = \left( x_4, y_4 , z_4 \right) $,其他端点下标作类似定义,不再赘述。
根据式$\eqref{正向运动学方程}$或图7可以很容易得到其中一个角度的解即:
$$ \lambda = \arctan \left( \frac{y}{x} \right) \label{方位角计算公式} \tag{5} $$
这里有一个需要注意的地方是,由于反三角函数是多值函数,所以函数值的确定必须谨慎,这会直接影响结果的一般性,因为当你选择其中一个函数值,那么就以为代入了一个范围条件,使得逆向运动学的求解是有范围的。分析反正切函数图像很容易可以知道,他的值域是$ \left( -\pi / 2 , \pi / 2 \right) $ ,而显然,我们的角度并不只这个狭窄的180度内存在,云台的旋转角是可能大于180度,甚至360度的。这里用的反正切三角函数并不是单纯的反正切,而是四象限反正切。即根据坐标 $\left( x , y\right) $所处的象限和反正切值综合确定正确的度数,其值范围扩大到了$ \left( -\pi , \pi \right) $。
参考图3,由于$P_4$坐标为已知量,且$P_4$与$P_2$的$z$坐标一致,即两点同高,因此可得:
$$ \begin{equation} \begin{cases} \begin{aligned} x_2 & = x_4 – \left( a_3 + a_4 \right) \cos \lambda \\ y_2 & = y_4 – \left( a_3 + a_4 \right) \sin \lambda \\ z_2 & = z_4 \end{aligned} \end{cases} \end{equation} \label{P_2坐标公式} \tag{6} $$
值得一提的是,这里求解有两条路径,一条是继续在三维空间中往下求解,另一种是对坐标进行逆变换,回到原来的侧视的二维坐标空间中进行运算。这两种路径对于单片机运算来说,运算量相差不大。重要:如果使用坐标变换先回到侧视二维坐标空间的话,切不可对$x_4$和$y_4$直接除以$\cos \lambda $ 和 $\sin \lambda $,这会导致结果病态。这一变换必须使用旋转矩阵的方法。
结果病态的原因
主要原因在于两点:1.运算精度有限。2.除以0
1.运算精度有限
假定运算精度为四位,原值为0.283,乘以$\cos \lambda = 0.01$,得到的结果为0.002。那么在逆向求解中,我试图通过0.002 除以$\cos \lambda $去复原正确值,会得到0.200这一结果。显然,产生接近41.5%的误差。
2.除以0
假定原值为1,乘以$\cos \frac{pi}{2} = 0$,得到的结果为0。如果我不采用旋转变换,那么是不可能根据两个零,复原出原值1的,而如果采用旋转变换(旋转了90度),很容易可以知道正确的结果。
本文采用的是直接三维空间坐标求解的方式。
图8. 逆向运动学分析几何图
已知$P_2$和$P_0$的坐标,即$P_0P_2$长度固定,又有$P_1P_2 = a_2 $和$P_1P_0 = a_1$为定值,因此该“三角形”唯一存在。(即使$\varphi_3$等于180度或大于180度)
根据余弦定理 ,易得:
$$ \begin{equation} \begin{cases} \begin{aligned}D_2 & = \sqrt{ x_2 ^2 +y_2^ 2 + z_2^2} \\ \varphi_1 & = \arccos \frac{a_1^2 + D_1^2 – a_2^2 }{2a_1D_1} \\ \varphi_3 & = \arccos \frac{a_1^2 + a_2^2 – D_1^2 }{2a_1a_1} \\ \varphi_2 & = \arctan \frac{z_2}{\sqrt{x_2^2 + y_2 ^ 2}} \end{aligned} \end{cases} \end{equation} \label{夹角求解公式} \tag{7} $$
其中,虽然反余弦三角函数也是多值函数,但是其主支的值域已经是$ \left( -\pi , \pi \right) $,包含了所有角度,可以使用。对于 $\varphi_2$的求取,这里的正切同样应当是四象限反正切,因为可能存在如下大于90度的情况。
图9. 大于90度的反例
当然,如果经过运动范围约束分析,发现角度不能大于90度也不能小于90度,其实也可以使用普通的反正切函数,要具体分析来看。
结合图6、图8进行角度分析可得:
$$ \begin{equation} \begin{cases} \begin{aligned} \angle b & = \varphi_1 + \varphi_2 \\ \angle s & = \pi – \varphi_1 – \varphi_2 – \varphi_3 \end{aligned} \end{cases} \end{equation} \label{夹角关系} \tag{8} $$
将式$\eqref{方位角计算公式}$ $\eqref{P_2坐标公式}$ $\eqref{夹角求解公式}$ $\eqref{夹角关系}$联立即可得到形如式$\eqref{一般逆向运动学公式}$的逆向运动学求解方程。根据该方程我们可以任意的确定达到各个空间坐标需要的舵机驱动角度,从而方便的实现精准的机械臂控制。
可行性分析
机械臂的运动学求解并非到这里就结束了,还有最关键的一步,即可行性分析。
这种可行性主要是物理的可行性,因为现实中的机械臂往往是有约束的,要考虑机械臂的任意两个臂会不会在空间上发生碰撞,角度是否在允许范围内等等,这需要结合具体的机械臂进行分析,而不能将其抽象成简单的直线了。
通过对图2所示机械臂的“摆弄”,其手臂不会发生碰撞,但关节角度有限制,其一是关节$P_2$不可反曲,其二是云台角度范围是-97°至137°。(实际上,云台角度大小取决于驱动电机的角度范围,我使用的舵机的实测运动角度范围是234度。而之所以最终范围是-97°至137°则取决于舵机的安装方法,也可以理解为零点的选取,这是根据我需要机器人抓持的范围而定的,并非随意的参数。如果你使用的是其他的专门云台驱动电机,例如步进电机、无刷电机等等,则可以获得无限角度的运动范围。假如不考虑机械臂碰到其他障碍物。)
最终经过分析得到各个角度的可行范围如下:
$$ \begin{equation} \begin{cases} \begin{aligned} \lambda & \in \left( -97^{\circ} , 137^{\circ} \right) \\ \beta & \in \left( 20^{\circ} , 155^{\circ} \right) \\ \angle b & \in \left( -15^{\circ} , 128^{\circ} \right) \\ \angle s & \in \left( -19.5^{\circ} , 116^{\circ} \right) \end{aligned} \end{cases} \end{equation} \label{角度范围} \tag{9} $$
基于单片机的C语言实现
验证分析
在进行C语言实现之前,我先使用MATLAB进行了仿真分析确保了结果的正确性。包括姿态分析、可达域分析、线性度分析、控制精度分析等等。
图10. 姿态分析
这一部分主要看看我公式的求解结果与使用URDF和MATLAB仿真工具的仿真结果是否一致。
图11. 可达域分析
这一部分主要分析了机械臂的运动范围,图中黑点均为可抵达的坐标,便于后续的轨迹规划分析。
图12. 线性度分析
这一部分主要分析了机械臂移动时角度变化的线性程度,可以看到线性程度并不是很理想,说明控制机械臂平移时如果对角度进行一次插值控制,可能导致末端移动轨迹变成曲线。毕竟平移时,角度不是一次函数变化。这说明了如果要控制机械臂水平移动必须依次计算起点到终点这条直线上各个点的逆运动学方程解,这会影响机械臂的控制方案,因为逆运动学求解是需要时间的,特别时在单片机这种平台上。 (本次将使用STM32F4系列的单片机进行实现,时钟频率168MHz,写完逆运动学求解代码后便立刻进行了计算时间的测试,最终测试得到的结果为为每毫秒100次运算)
图13. 控制精度分析图
本例使用驱动舵机的虚位约在7us,舵机虚位值得是舵机控制信号响应的阈值,7us以内的信号变化可能不会反映在驱动上,表现结果就是舵机不动。上图是每次移动3~5mm绘制得到的条形图,说明舵机驱动的机械臂在不考虑机械关节虚位的情况下,理论最大精度是5mm。(后面实测发现精度约在8mm,而在一些边缘角度甚至出现了大距离偏差,猜测是舵机位置闭环的非线性导致的,这说明了什么?想要更高的控制精度就不能用舵机)。
这些分析对控制思路有一定的影响,但具体的分析代码不是本文重点,需要的可以从如下云存储中下载。
文件名:机械臂姿态解算及其分析.zip
运动学求解算法的实现
首先是进行函数的声明和结构体的定义,由于需要使用坐标向量,角度向量等参数,为使得函数的参数更加简洁,使用了结构体对坐标和角度进行了定义。
函数声明及结构体定义
/**
* @brief 机械臂空间坐标向量
* 坐标系以云台中心为原点,x轴水平向前,y轴水平向左,z轴竖直向上。
* 云台绕z轴旋转。
* 单位:mm
*/
typedef struct
{
int16_t x, y, z;
}ArmVector_t;
/**
* @brief 四自由度机械臂每个关节的角度
* yaw为云台角度
* bigArm为大臂的关节角
* smallArm为小臂的关节角
* hand为机械手的关节角
* 单位:rad
*/
typedef struct
{
float yaw, bigArm, smallArm, hand;
}ArmAngle_t;
/**
* @brief 机械臂正向运动学求解函数,通过各个关节角的角度计算机械臂末端所处的位置
* @param angle 关节角度结构体 作为函数的传入参数,求解函数将基于该结构体内的关节角度进行计算
* @param vector 位置向量结构体 作为函数的传出参数,包含机械臂末端位置向量
* @retval isLegal 表征该关节角在物理上是否合法,当不合法时计算的位置将均为零。返回值为1是表示物理上合法。
*/
uint8_t CalArmVector(const ArmAngle_t *angle, ArmVector_t *vector);
/**
* @brief 机械臂逆运动学求解函数,通过末端位置向量计算各个关节角的角度
* @param vector 位置向量结构体 作为函数的传入参数,求解函数将基于该结构体内的位置坐标进行计算
* @param angle 关节角度结构体 作为函数的传出参数,包含各个关节角的角度
* @retval isreachable 表征该位置在物理上是否可达,当不可达时计算的角度将均为零。返回值为1是表示物理上可达。
*/
uint8_t CalArmAngle(const ArmVector_t *vector, ArmAngle_t *angle);
以下为具体的函数定义,对前述的公式进行了实现,其中关于四象限反正切,math库有提供atan2f函数可以使用。
函数定义
/**
* @brief 机械臂正向运动学求解函数,通过各个关节角的角度计算机械臂末端所处的位置
* @param angle 关节角度结构体
* 作为函数的传入参数,求解函数将基于该结构体内的关节角度进行计算
* @param vector 位置向量结构体
* 作为函数的传出参数,包含机械臂末端位置向量
* @retval isLegal 表征该关节角在物理上是否合法,当不合法时计算的位置将均为零。返回值为1是表示物理上合法。
*/
uint8_t CalArmVector(const ArmAngle_t* angle, ArmVector_t* vector){
/* 变量记录与定义 */
float lambda = angle->yaw;
float bigArmAngle = angle->bigArm;
float smallArmAngle = angle->smallArm;
float phi3 = PI - (bigArmAngle + smallArmAngle);
/* 关节角度物理合法性检验 */
if ( ( lambda < YAW_ANGLE_LOW / 180.0f * PI || lambda > YAW_ANGLE_UP / 180.0f * PI ||
bigArmAngle < BIG_ARM_ANGLE_LOW / 180.0f * PI || bigArmAngle > BIG_ARM_ANGLE_UP / 180.0f * PI ||
phi3 < INC_ARM_ANGLE_LOW / 180.0f * PI || phi3 > INC_ARM_ANGLE_UP / 180.0f * PI ||
smallArmAngle < SMALL_ARM_ANGLE_LOW / 180.0f * PI || smallArmAngle > SMALL_ARM_ANGLE_UP / 180.0f * PI) ){
vector->x = 0;
vector->y = 0;
vector->z = 0;
return 0;
}
/* 公式计算末端位置向量 */
float distance = armLength[0] * cosf(bigArmAngle) + armLength[1] * cosf(smallArmAngle) + armLength[2];
vector->x = (int16_t)(distance * cosf(lambda) * 1000);
vector->y = (int16_t)(distance * sinf(lambda) * 1000);
vector->z = (int16_t)((armLength[0] * sinf(bigArmAngle) - armLength[1] * sinf(smallArmAngle)) * 1000);
return 1;
}
/**
* @brief 机械臂逆运动学求解函数,通过末端位置向量计算各个关节角的角度
* @param vector 位置向量结构体
* 作为函数的传入参数,求解函数将基于该结构体内的位置坐标进行计算
* @param angle 关节角度结构体
* 作为函数的传出参数,包含各个关节角的角度
* @retval isreachable 表征该位置在物理上是否可达,当不可达时计算的角度将均为零。返回值为1是表示物理上可达。
*/
uint8_t CalArmAngle(const ArmVector_t* vector, ArmAngle_t* angle){
/* 向量单位转换 */
float x = 1.0f * (vector->x) / 1000;
float y = 1.0f * (vector->y) / 1000;
float z = 1.0f * (vector->z) / 1000;
/* 计算四象限反正切 求得 lambda */
float lambda = atan2f(y, x);
/* 推算第二关节角度 */
float x2 = x - armLength[2] * cosf(lambda);
float y2 = y - armLength[2] * sinf(lambda);
float z2 = z;
/* 计算第二关节位置向量的模长 */
float D1 = sqrtf(x2 * x2 + y2 * y2 + z2 * z2);
/* 正弦定理计算关节夹角 */
float phi1 = acosf((armLength[0] * armLength[0] + D1 * D1 - armLength[1] * armLength[1]) / (2 * armLength[0] * D1));
float phi2 = atan2f(z2, sqrtf(x2 * x2 + y2 * y2));
float phi3 = acosf((armLength[0] * armLength[0] + armLength[1] * armLength[1] - D1 * D1) / (2 * armLength[0] * armLength[1]));
/* 计算大臂关节角 */
float bigArmAngle = phi1 + phi2;
/* 计算小臂关节角 */
float smallArmAngle = PI - bigArmAngle - phi3;
/* 关节角度物理可行性检验 */
if ( ( lambda < YAW_ANGLE_LOW / 180.0f * PI || lambda > YAW_ANGLE_UP / 180.0f * PI ||
bigArmAngle < BIG_ARM_ANGLE_LOW / 180.0f * PI || bigArmAngle > BIG_ARM_ANGLE_UP / 180.0f * PI ||
phi3 < INC_ARM_ANGLE_LOW / 180.0f * PI || phi3 > INC_ARM_ANGLE_UP / 180.0f * PI ||
smallArmAngle < SMALL_ARM_ANGLE_LOW / 180.0f * PI || smallArmAngle > SMALL_ARM_ANGLE_UP / 180.0f * PI) ){
/* 若物理不可行则置零结果值再返回 */
angle->yaw = 0;
angle->bigArm = 0;
angle->smallArm = 0;
/* 物理不可行则返回值为零 */
return 0;
}
/* 保存结果值 */
angle->yaw = lambda;
angle->bigArm = bigArmAngle;
angle->smallArm = smallArmAngle;
return 1;
}
机械臂控制算法的实现
将算法落实到实现,还剩最后一个重要一环,即控制量的转换。在本例中就是如何将算法的输出结果(角度)转换为能被舵机接收的控制信号。
其中主要涉及到两点:
关于放大系数的确定,其实就是一个角度到舵机信号脉宽的一次函数映射关系。例如0度对应舵机信号脉宽500μs,180度对应舵机信号脉宽2500μs,那么这一放大系数就是11.11μs/度。虽然相关信息在舵机的参数面板中已经给出,但我发现与实际情况有不小的偏差,即舵机的角度范围并不严格刚好是180度(而且据说边缘似乎有非线性现象?)。于是,我通过逐点测量和最小二乘法 拟合出误差更小的映射函数,并取其斜率作为放大倍数。由于先前角度选取的一致性(逆时针为正),我们会发现所有的放大系数均是正数。
关于零位的确定,主要是指当$\lambda$、$\angle b$、$\angle s$为零时,对应的舵机驱动角度和信号,毕竟为了移动范围合适,我不会刚刚好把舵机的中央位置安装在这些角度为零的时候,又或者购买的整机机械臂的角度和我们的设计有一点出入。
以下是相关物理参数的宏定义,包括信号的转换,机械臂的长度,角度范围限制等等。
相关物理参数的宏定义
/*
************************************************
* 机械臂物理结构校准及零点校准部分
************************************************
*/
/**
* @brief 机械臂各个结构的长度
* 从左至右分别为 大臂 小臂 手腕关节至手掌中心的长度 手掌大小
* 单位:m
*/
/* 大臂 小臂 手腕关节至手掌中心 手掌大小 */
#define ARM_STRUCT_LENGTH { 0.147f , 0.160f , 0.170f , 0.060f }
/**
* @brief 舵机角度控制的转换系数
* 单位:us/度
*/
/* 云台 servoID = 0 */
#define YAW_SERVO_US_PER_ANGLE ( 8.105f)
/* 大臂 servoID = 1 */
#define BIG_ARM_SERVO_US_PER_ANGLE (10.000f)
/* 小臂 servoID = 2 */
#define SMALL_ARM_SERVO_US_PER_ANGLE (11.589f)
/* 机械手 servoID = 3 */
#define HAND_SERVO_US_PER_ANGLE (11.111f)
/**
* @brief 机械臂关节角度零点偏移校准
*/
/* 云台 */
#define YAW_ARM_ANGLE_ZERO (( 1308 ))
/* 大臂 */
#define BIG_ARM_ANGLE_ZERO (( 700 ))
/* 小臂 */
#define SMALL_ARM_ANGLE_ZERO (( 900 ))
/* 机械手 */
#define HAND_ARM_ANGLE_ZERO (( 1000 ))
/**
* @brief 机械臂关节角度范围
* 单位:度
*/
/* 云台范围 */
#define YAW_ANGLE_UP (137.0f)
#define YAW_ANGLE_LOW (-97.0f)
/* 大臂 */
#define BIG_ARM_ANGLE_UP (128.0f)
#define BIG_ARM_ANGLE_LOW (-15.0f)
/* 小臂 */
#define SMALL_ARM_ANGLE_UP (116.0f)
#define SMALL_ARM_ANGLE_LOW (-19.5f)
/* 两臂夹角 */
#define INC_ARM_ANGLE_UP (160.0f)
#define INC_ARM_ANGLE_LOW (25.0f)
/* 机械手 */
#define HAND_ANGLE_UP (102.0f)
#define HAND_ANGLE_LOW (0.0f)
根据上述分析,我们可以得到如下转换函数:
控制脉冲转换函数
/**
* @brief 将机械臂关节角转换为舵机控制脉冲
* @param servoID 舵机ID,亦即关节ID
* @param angle 角度(弧度制)
* @retval 脉冲宽度(单位us)
*/
uint16_t ArmAngleToPulse(uint8_t servoID, float angle){
uint16_t pulse = 0;
switch(servoID){
case 0 :
pulse = (angle) / PI * 180 * YAW_SERVO_US_PER_ANGLE + YAW_ARM_ANGLE_ZERO;
break;
case 1 :
pulse = (angle) / PI * 180 * BIG_ARM_SERVO_US_PER_ANGLE + BIG_ARM_ANGLE_ZERO;
break;
case 2 :
pulse = (angle) / PI * 180 * SMALL_ARM_SERVO_US_PER_ANGLE + SMALL_ARM_ANGLE_ZERO;
break;
case 3 :
pulse = (angle) / PI * 180 * HAND_SERVO_US_PER_ANGLE + HAND_ARM_ANGLE_ZERO;
break;
default:
break;
}
return pulse;
}
有了以上基础后,我们可以进行机械臂控制器的设计,期望主要包含以下内容:
状态机的设计便于控制的实现,更重要的是因为机械臂的移动不是瞬间的过程,我们需要区分机械臂的空闲状态、就绪状态、移动状态,从而执行不同的逻辑。
轨迹规划则是自动的控制其从A点移动到B点或者说是从当前点移动的新的一点,我们需要一套算法自动的规划这一过程并判断是否能移动过去,如果不能则执行错误代码返回。
实时控制则是处于多线程的考虑,我们期望在机器人的运行过程中,在移动机械臂的同时做一些其他的事情,毕竟机械臂的移动不需要占用CPU多少时钟。
以下是相关的定义代码,具体意思已经在注释中注明,本处不再赘述。其中关于精细度的部分,这一设计的目的是因为我将一条轨迹划分为若干段
机械臂控制器结构体
typedef enum{
ARM_DILE = 0 ,
ARM_READY,
ARM_MOTION
}ArmState_e;
/**
* @brief 机械臂控制器结构体
* 用于记录机械臂的状态变量和各类输入输出变量
*/
typedef struct{
/* --- 状态控制部分 --- */
/* 机械臂当前状态 */
ArmState_e armCurState;
/* 机械臂当前位置*/
/* 为降低解算开销,该位置不记录移动过程中的位置,因此在移动过程中改变量不可靠 */
ArmVector_t armCurPostion;
/* 机械臂当前关节角 */
ArmAngle_t armCurAngle;
uint8_t posFlag;
/* --- 细分控制部分 --- */
ArmAngle_t armAngleUnit[ARM_MAX_DIVISION];
uint8_t totalNumber;
uint8_t currentNumber;
}ArmController;
机械臂控制器的相关宏定义
/*
************************************************
* 机械臂控制参数
************************************************
*/
/* 机械臂初始位置 单位mm x y z */
#define ARM_INIT_POSITION { -170 , 180 , -20}
/**
* @brief 机械臂移动细分最大值
* 该参数决定了机械臂移动的精细程度,表示一次移动最多会被细分成多少次进行
* 注意:细分度占用内存空间,若细分度过大可能导致内存不足,建议细分最大值在100以下。
*/
#define ARM_MAX_DIVISION (100)
/**
* @brief 机械臂移动速度 单位 mm/s
* 该参数决定了机械臂默认的移动速度,与细分最大值共同决定了一次移动的细分程度
*/
#define ARM_MOVE_SPEED (200)
/**
* @brief 机械臂控制周期 单位 ms
* 该参数决定了机械臂一次细分后的移动响应需要的时间
* 舵机控制信号为T=20ms的脉冲,因此不建议控制周期小于1~2T
* 如果不存在影子寄存器可能出现无法预料的结果
*/
#define ARM_CONTROLLER_PERIOD (50) //机械臂控制周期
轨迹规划器的设计代码
/**
* @brief 设置机械臂目标点函数
* @param vector 目标位置向量
* @retval 目标是否可达。
* 若目标不可达则返回0,且机械臂保持不动。
* 若目标可达则返回1,表示设置成功。
*
* 错误代码 2 表示机械臂正在移动中,请等待移动完成
*
*/
uint8_t SetArmTarget(const ArmVector_t *vector, ArmPlaning_e armPlan){
ArmAngle_t armAngle;
/* 机械臂正在运动 */
if(armController.armCurState != ARM_DILE){
return 2;
}
/* 目标检验不通过,目标不可达 */
if(!CalArmAngle(vector,&armAngle)){
return 0;
}
switch (armPlan){
case ARM_LINEAR_PATH: {
/* 计算移动距离 */
int32_t distance = (int32_t)sqrtf(powf((float)(vector->x - armController.armCurPostion.x), 2) +
powf((float)(vector->y - armController.armCurPostion.y), 2) +
powf((float)(vector->z - armController.armCurPostion.z), 2));
/* 计算细分度 */
/* 细分度 = 需要的控制周期数 = 距离 / 速度 / 每周期时间 */
uint8_t div = (uint8_t)(distance * 1000 / ARM_MOVE_SPEED / ARM_CONTROLLER_PERIOD);
/* 细分度最大值幅限 */
if(div > ARM_MAX_DIVISION){
div = ARM_MAX_DIVISION;
}
/* 细分角度分配 */
ArmVector_t vectorUnit;
ArmAngle_t angleUnit;
armController.totalNumber = 0; /* 细分控制栈置空 */
for (uint8_t i = 1; i <= div;i++){
vectorUnit.x = (int16_t)((int32_t)(vector->x - armController.armCurPostion.x) * i / div) + armController.armCurPostion.x;
vectorUnit.y = (int16_t)((int32_t)(vector->y - armController.armCurPostion.y) * i / div) + armController.armCurPostion.y;
vectorUnit.z = (int16_t)((int32_t)(vector->z - armController.armCurPostion.z) * i / div) + armController.armCurPostion.z;
/* 路径检验不通过,路径有障碍 */
if(!CalArmAngle(&vectorUnit,&angleUnit)){
return 0;
}
armController.armAngleUnit[armController.totalNumber++] = angleUnit;
}
armController.currentNumber = 0;
break;
}
case ARM_CURVE_PATH:{
/* 计算四象限反正切 求得 Lambda */
float currentLambda = atan2f(armController.armCurPostion.y, armController.armCurPostion.x);
float targetLambda = atan2f(vector->y, vector->x);
/* 计算臂长投影 */
float armLenthInXOY = sqrtf(powf(armController.armCurPostion.x, 2) + powf(armController.armCurPostion.y, 2));
/* 计算圆弧细分度 */
/* 细分度 = 需要的控制周期数 = 弧长 / 速度 / 每周期时间 */
uint16_t curveDiv = (uint8_t)(fabs(targetLambda - currentLambda) * armLenthInXOY / 2 * 1000 / ARM_MOVE_SPEED / ARM_CONTROLLER_PERIOD);
/* 计算中间位置 */
ArmAngle_t midAngle = {targetLambda, armController.armCurAngle.bigArm, armController.armCurAngle.smallArm, armController.armCurAngle.hand};
ArmVector_t midVector;
if(!CalArmVector(&midAngle, &midVector)){ /* 路径检验不通过,路径有障碍 */
return 0;
}
/* 计算直线距离 */
int32_t distance = (int32_t)sqrtf(powf((float)(vector->x - midVector.x), 2) +
powf((float)(vector->y - midVector.y), 2) +
powf((float)(vector->z - midVector.z), 2));
/* 计算直线细分度 */
uint16_t div = (uint8_t)(distance * 1000 / ARM_MOVE_SPEED / ARM_CONTROLLER_PERIOD);
/* 细分度最大值幅限 */
if(curveDiv + div > ARM_MAX_DIVISION){
curveDiv = curveDiv * ARM_MAX_DIVISION / (curveDiv + div) ;
div = ARM_MAX_DIVISION - curveDiv;
}
/* 细分角度分配 */
ArmVector_t vectorUnit;
ArmAngle_t angleUnit;
armController.totalNumber = 0; /* 细分控制栈置空 */
angleUnit.bigArm = armController.armCurAngle.bigArm;
angleUnit.smallArm = armController.armCurAngle.smallArm;
angleUnit.hand = armController.armCurAngle.hand;
for (uint8_t i = 1; i <= curveDiv; i++){
angleUnit.yaw = (targetLambda - currentLambda) * i / curveDiv + currentLambda;
/* 路径检验不通过,路径有障碍 */
if(!CalArmVector(&angleUnit,&vectorUnit)){
return 0;
}
armController.armAngleUnit[armController.totalNumber++] = angleUnit;
}
for (uint8_t i = 1; i <= div;i++){
vectorUnit.x = (int16_t)((int32_t)(vector->x - midVector.x) * i / div) + midVector.x;
vectorUnit.y = (int16_t)((int32_t)(vector->y - midVector.y) * i / div) + midVector.y;
vectorUnit.z = (int16_t)((int32_t)(vector->z - midVector.z) * i / div) + midVector.z;
/* 路径检验不通过,路径有障碍 */
if(!CalArmAngle(&vectorUnit,&angleUnit)){
return 0;
}
armController.armAngleUnit[armController.totalNumber++] = angleUnit;
}
armController.currentNumber = 0;
break;
}
default:
break;
}
/* 机械臂运动准备好 */
armController.armCurState = ARM_READY;
armController.armCurPostion = *vector;
armController.armCurAngle = armAngle;
return 1;
}
/**
* @brief 强制重置机械臂目标位置,该状态下不进行平滑移动,而是直接性的位置重置,细分度为1
* @param vector 目标位置向量
* @retval 目标是否可达。
* 若目标不可达则反应0,且机械臂保持不动。
*/
uint8_t EnforceArmTarget(const ArmVector_t *vector){
ArmAngle_t armAngle;
/* 目标检验不通过,目标不可达 */
if(!CalArmAngle(vector,&armAngle)){
return 0;
}
/* 设置机械臂位置 */
SetServoPWM(0,ArmAngleToPulse(0, armAngle.yaw));
SetServoPWM(1,ArmAngleToPulse(1, armAngle.bigArm));
SetServoPWM(2,ArmAngleToPulse(2, armAngle.smallArm));
SetServoPWM(3,ArmAngleToPulse(3, armAngle.hand));
/* 状态更新 */
armController.armCurPostion = *vector;
armController.armCurAngle = armAngle;
return 1;
}
实时控制器的设计代码
/**
* @brief: 更新机械臂姿态任务,请将该函数在任务调度器或者相关多线程系统中
* 以ARM_CONTROLLER_PERIOD为周期进行循环调用
* @param:
* @retval:
*/
uint8_t UpdateArmPosTask(uint8_t info){
if(info==0)
return 0;
/* 机械臂空闲,无需移动 */
if(armController.armCurState == ARM_DILE){
return 0;
}
/* 机械臂准备好状态 变更为移动状态 */
if(armController.armCurState == ARM_READY){
armController.armCurState = ARM_MOTION;
}
if(armController.armCurState == ARM_MOTION){
if(armController.currentNumber < armController.totalNumber ){
/* 设置机械臂位置 */
SetServoPWM(0,ArmAngleToPulse(0, armController.armAngleUnit[armController.currentNumber].yaw));
SetServoPWM(1,ArmAngleToPulse(1, armController.armAngleUnit[armController.currentNumber].bigArm));
SetServoPWM(2,ArmAngleToPulse(2, armController.armAngleUnit[armController.currentNumber].smallArm));
SetServoPWM(3,ArmAngleToPulse(3, armController.armAngleUnit[armController.currentNumber].hand));
/* 状态更新 */
armController.armCurAngle = armController.armAngleUnit[armController.currentNumber++];
}else{
/* 移动完成,机械臂进入空闲状态 */
armController.armCurState = ARM_DILE;
}
}
return 0;
}
/**
* @brief: 获取机械臂当前状态
* @retval: 机械臂状态 ready就绪 / motion运动中
*/
ArmState_e GetArmState(void){
return (armController.armCurState);
}
效果演示
由于夹持的时候忘记让机械手握住笔的底端,导致笔晃来晃去,本来可以更好一点。
以下是机械臂曲线规划演示。
附录
附录A
MATLAB对式$\eqref{正向运动学方程二维}$的三角函数部分(去掉末尾常数项)直接进行逆向求解得到计算式如下,实际上,对$\eqref{正向运动学方程}$的求解运行了数分钟也没有结果,这种情况可能是因为我用法不对,因为也许三角函数可以看成一个整体?或者对MATLAB的求解加以其他限制,例如范围等等,毕竟由于机械结构的限制,每个关节角的范围必定在$\left[ -\pi , \pi \right)$之间。
$$ \begin{aligned} & \left(\begin{aligned} -2\,\mathrm{atan}\left(\frac{\frac{{A_2 }^2 \,\sigma_4 }{\sigma_1 }-2\,A_2 \,z_2 -\frac{{A_1 }^2 \,\sigma_4 }{\sigma_1 }-2\,A_1 \,z_2 +\frac{{y_2 }^2 \,\sigma_4 }{\sigma_1 }+\frac{{z_2 }^2 \,\sigma_4 }{\sigma_1 }+\frac{2\,A_2 \,y_2 \,\sigma_4 }{\sigma_1 }}{\sigma_2 }\right)\\ -2\,\mathrm{atan}\left(\frac{\frac{{A_2 }^2 \,\sigma_3 }{\sigma_1 }-2\,A_2 \,z_2 -\frac{{A_1 }^2 \,\sigma_3 }{\sigma_1 }-2\,A_1 \,z_2 +\frac{{y_2 }^2 \,\sigma_3 }{\sigma_1 }+\frac{{z_2 }^2 \,\sigma_3 }{\sigma_1 }+\frac{2\,A_2 \,y_2 \,\sigma_3 }{\sigma_1 }}{\sigma_2 }\right) \end{aligned}\right)\\ \mathrm{}\\ & \textrm{where}\\ \mathrm{}\\ & \;\;\sigma_1 =-{A_1 }^2 +{A_2 }^2 +2\,A_2 \,y_2 +{y_2 }^2 +{z_2 }^2 \\ \mathrm{}\\ & \;\;\sigma_2 ={A_1 }^2 +2\,A_1 \,y_2 -{A_2 }^2 +{y_2 }^2 +{z_2 }^2 \\ \mathrm{}\\ & \;\;\sigma_3 =2\,A_2 \,z_2 -\sigma_5 \\ \mathrm{}\\ & \;\;\sigma_4 =2\,A_2 \,z_2 +\sigma_5 \\ \mathrm{}\\ & \;\;\sigma_5 =\sqrt{{\left({A_1 }^2 +2\,A_1 \,A_2 +{A_2 }^2 -{y_2 }^2 -{z_2 }^2 \right)}\,{\left(-{A_1 }^2 +2\,A_1 \,A_2 -{A_2 }^2 +{y_2 }^2 +{z_2 }^2 \right)}} \end{aligned} $$



My brother suggested I might like this website He was totally right This post actually made my day You cannt imagine just how much time I had spent for this information Thanks